Bảng công thức nguyên hàm chi tiết và đầy đủ nhất
Nội dung chính
Định nghĩa và công thức tính nguyên hàm
Định nghĩa
Cho một hàm số f(x) xác định trên K (K là khoảng, đoạn hay nửa khoảng). Hàm số F(x) sẽ được gọi là nguyên hàm của hàm số f(x) trên K nếu F'(x) = f(x) với mọi x ∈ K.
Kí hiệu: ∫ f(x)dx = F(x) + C.
Định lý
1) Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì tương ứng với mỗi hằng số C, hàm số G(x) = F(x) + C cũng là một nguyên hàm của f(x) trên K.
2) Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì tất cả nguyên hàm của f(x) trên K cũng đều có dạng F(x) + C, với C là một hằng số.
Vì vậy, F(x) + C; C ∈ R là họ tất cả các nguyên hàm của f(x) trên K.
Tìm hiểu một số thông tin về nguyên hàm
Tính chất của nguyên hàm
- (∫ f(x)dx)’ = f(x) và ∫ f'(x)dx = f(x) + C.
- Nếu F(x) có đạo hàm thì: ∫d(F(x)) = F(x) + C).
- ∫ kf(x)dx = k∫ f(x)dx với điều kiện k là hằng số khác 0.
- ∫[f(x) ± g(x)]dx = ∫ f(x)dx ± ∫g(x)dx
Sự tồn tại của nguyên hàm
Định lí: Mọi hàm số f(x) liên tục trên K cũng đều có nguyên hàm trên K
Bảng công thức nguyên hàm cơ bản của các hàm số thường gặp
Đây là bảng công thức nguyên hàm cơ bản nhất
Phương pháp tính nguyên hàm
Có những phương pháp dùng để tính nguyên hàm như sau:
Phương pháp chuyển đổi
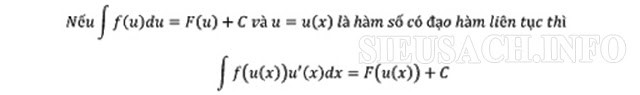
Tính nguyên hàm theo phương pháp chuyển đổi
Hệ quả:
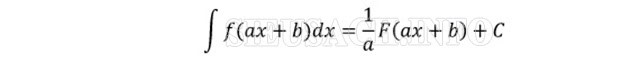
Đây là công thức hệ quả của hàm số trên
Áp dụng công thức hệ quả trên, chúng ta có bảng nguyên hàm mở rộng dưới đây:
Bảng công thức nguyên hàm được suy ra từ hệ quả
Phương pháp tính theo nguyên hàm từng phần
Bước 1: Chúng ta biến đổi tích phân ban đầu về dạng: I = ∫ f(x)dx = ∫ f1(x).f2(x)dx
Bước 2: Đặt:
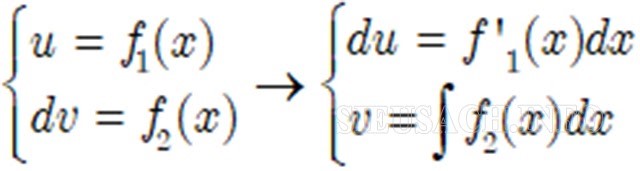
Bước 2 các bạn làm như hướng dẫn trên hình ảnh
Bước 3: Khi đó: ∫u.dv = u.v – ∫v.du
Lưu ý những lỗi dễ gặp khi giải toán nguyên hàm
Nhớ nhầm công thức nguyên hàm
Nguyên nhân: nền tảng của nguyên hàm chính là đạo hàm. Vì vậy, để giải được nguyên hàm thì trước tiên bạn cần nắm vững đạo hàm trước đã. Nếu bạn chưa hiểu rõ bản chất và nắm vững kiến thức của hai nguyên hàm và đạo hàm thì rất dễ bị nhầm lẫn với nhau.
Khắc phục: học thật vững bảng nguyên hàm cơ bản. Đồng thời luyện tập thói quen kiểm tra công thức: lấy đạo hàm của nguyên hàm tìm được xem có khớp số đề cho hay không.
Vận dụng không đúng định nghĩa tích phân
Để không mắc phải lỗi này, bạn cần tạo thói quen khi tính ∫f(x)dx nhớ chú ý kiểm tra xem hàm số y = f(x) có liên tục ở trên đoạn hay không. Lưu ý, nếu hàm số không liên tục trên đoạn thì nghĩa là tích phân đó không tồn tại!
Nhớ nhầm tính chất tích phân, nguyên hàm
Thay vì sử dụng công thức tích phân từng phần thì nhiều bạn thường tự sáng tạo ra quy tắc nguyên hàm của một tích. Lỗi sai này rất nghiêm trọng và rất phổ biến.
Có 4 lỗi thường gặp khi giải nguyên hàm
Vận dụng sai công thức tính nguyên hàm
Các dạng đề và công thức bảng nguyên hàm rất nhiều. Nên nhiều trường hợp các bạn học sinh áp dụng sai công thức, hoặc nhớ nhầm từ công thức này sang công thức kia
Khắc phục: Cần cẩn thận và tỉ mỉ là một yếu tố cực kỳ cần thiết trong môn toán Bởi chỉ cần sai một con số nhỏ hoặc một công thức nhỏ trong bảng nguyên hàm nói riêng cũng như trong các bài toán nói chung thì mọi kết quả sẽ trở nên công cốc.
Vì thế một lần nữa lời khuyên dành cho cách khắc phục những lỗi sai này là học thuộc vững bảng nguyên hàm và công thức nguyên hàm cơ bản. Hiểu đúng dạng đề để tránh việc sử dụng sai công thức.
Hy vọng với những thông tin chúng tôi chia sẻ về bảng nguyên hàm ở bài viết trên sẽ phần nào giúp được các sĩ tử trong việc học tập và thi cử. Chúc các sĩ tử đạt kết quả cao trong kì thi Trung học phổ thông quốc gia sắp tới!
Xem thêm:
- Bảng hóa trị hóa học & mẹo học thuộc bảng hóa trị nhanh nhất
- Cấp số cộng cấp số nhân là gì? Định nghĩa, tính chất và bài tập
- Số nguyên tố là gì? Những khái niệm liên quan đến số nguyên tố
- Hiệu suất là gì? Công thức tính hiệu suất
- Ứng suất là gì? Nguyên nhân tạo ra ứng suất
Tôi là Nguyễn Tiến Thành – Tôi đã có nhiều năm kinh nghiệm review đánh giá các loại thiết bị vệ sinh công nghiệp và các mẹo làm sạch. Hy vọng những chia sẻ của tôi sẽ đem lại cho các bạn những thông tin hữu ích hơn.
